|
Monte Carlo シミュレーション例: 信頼区間の精度 |

|

|

|

|
|
|
Monte Carlo シミュレーション例: 信頼区間の精度 |

|

|

|

|
Monte Carlo シミュレーション例: 信頼区間の精度
概要
非線形回帰で曲線をフィットする際、最も重要な結果セットの 1 つはパラメーターの 95% 信頼区間です。これらの区間は、いくつかの数学的単純化に基づく標準誤差から算出されます。これらは "漸近" または "近似" 標準誤差と呼ばれます。数式が線形であると仮定して算出されますが、非線形数式の場合にも適用されます。この単純化は、この区間は楽観的すぎたり、狭すぎることがあるため、真の信頼度は 95% 未満であるということを意味します。
区間が本当に 95% の信頼度を示しているかどうかはどうしたらわかるのでしょうか?これに答える一般的な方法はありません。しかし、特定の状況においては、シミュレーションを使用して答えを導くことができます。このページでは、Prism 6 で新しく導入された Monte Carlo シミュレーション機能を使用してこれを行う方法について説明します。ここでは、用量反応曲線をシミュレーションし、ヒル スロープの 95% 信頼区間の精度を検証します。Christopolous は、ヒル スロープの分布は非対称になることもあり得るため、代わりにヒル スロープの対数をフィットするように提案しています (1)。
ステップ 1: 最初の実験のシミュレーション
任意の個所で、「新規」[New]...「新規の分析」[New Analysis] をクリックし、「シミュレーション」[Simulate data]...「XYデータのシミュレーション」[Simulate XY Data] を選択します。この例に正確に従うには、以下のオプションを選択します。
| • | 「X値」[X values] タブ: X=-9 の位置から、X が -3.0 以上になるまで 0.5 ずつ各 X 値を増やします。 |
| • | 「数式」[Equation] タブ: 「用量反応 - 刺激」[Dose-response - Stimulation] フォルダーを選択し、「log(agonist) vs.反応 -- 可変傾斜」[log(agonist) vs. response --Variable slope] の数式を選択します。 |
| • | 「パラメータ値」[Parameter values] タブ: 3 つの繰り返し値を使用して 1 つのデータ セットのシミュレーションを行うことを選択します。Bottom=250、Top=5000、ogEC50=-6、HillSlope=0.5 に設定します。 |
| • | 「偶然誤差」[Random error] タブ: 偶然誤差は「ガウス分布 絶対」[Gaussian, absolute] で、SD=200 です。 |
ステップ 2: 最初の実験のフィット
| 1. | グラフから、「分析」[Analyze] をクリックし、「非線形回帰」[Nonlinear regression] を選択します。または、ツールバーの 「分析」[Analysis] セクションにある非線形回帰ショートカット ボタンをクリックします。 |
| 2. | 最初の「フィット」[Fit] タブで 「用量反応 - 刺激」[Dose-response - Stimulation] フォルダーを選択します。続いて、「log(agonist) vs.反応 -- 可変傾斜」[log(agonist) vs. response --Variable slope] 数式を選択します。残りのタブはすべてデフォルトのままにします。 |
| 3. | 「OK」 をクリックすると、データにモデルがフィットされ、グラフ上に曲線がプロットされます。 |
ステップ 3: 他の 2、3 のデータ セットのシミュレーション
ヒル スロープ (このシミュレーションで検証するパラメーター)に注意してください。異なる乱数を使用して新しいデータをシミュレーションするには、赤色のサイコロのアイコンをクリックするか、「変更」[Change] メニューを表示して [Simulate Again] を選択します。ヒル スロープが変わったことに注目してください。
ステップ 4: さらに多くのデータ セットのシミュレーション
非線形回帰結果で 「分析」[Analyze] をクリックし、「シミュレーション」[Simulate data]...「モンテカルロ」[Monte-Carlo] を選択します。
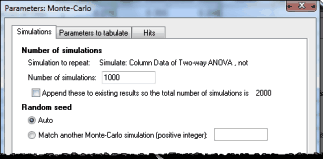
最初の 「シミュレーション」[Simulations] タブで、実行するシミュレーション回数を選択します。たとえば「1000」と入力します。
2 番目の 「出力するパラメータ」[Parameters to tabulate] タブで、表形式にするパラメーターを選択します。Prism によってデータの分析時に作成される分析定数のリストから選択します。たとえば、ヒル スロープの場合は 2 つの信頼限界のみを表形式にします。
3 番目の「ヒット」[Hits] タブで、特定のシミュレーション結果を "ヒット" と見なす基準を定義します。この例では、ヒットは信頼区間の範囲に真の値 0.5 (シミュレーションで設定) が含まれることと定義します。つまり、ヒットは下限値が 0.5 以下で上限値が 0.5 以上であることと定義されます。

「OK」 をクリックすると、シミュレーションが実行されます。コンピューターの速度により、数秒から数十秒かかります。
ステップ 5: Monte-Carlo シミュレーションの結果
シミュレーションの結果が 1 つのページに表示されます (上記の 「ヒット」[Hits] タブで個別のシミュレーションのレポート オプションをすべてオフにしたため)。
ヒットの割合は 0954 です。この例では、"ヒット" は、真のパラメーター値が信頼区間に含まれることと定義しました。つまり、1000 のシミュレーション データ セットの 95.4% で、ヒル スロープの信頼区間に真の値 (シミュレーションで使用されたもの) が含まれています (これらの結果は Prism で生成された乱数に基づくため、この例に従った場合、多少結果は異なります)。これは、まさに95% 信頼区間であり、この実験デザインの信頼区間は信頼できることを意味します。この実験デザインの場合、代わりにヒル スロープの対数のフィットを検討する必要はありません。
ステップ 6: 他の値の試行
この結果の信頼区間が広すぎる (93.9% から 96.6%) と感じられる場合は、Monte Carlo シミュレーションをもっと多くの回数やり直します (10,000 など) 。
結果は、実験デザインと選択したパラメーター値に特定のものです。シミュレーションに戻り、ヒル スロープを 4.0 に変更します。[Monte Carlo] ダイアログで、"ヒット" は信頼区間が真の値 4.0 を含むことと再定義します。ヒットは下限値が 4.0 以下で上限値は 4.0 以上であると定義されます。そのような急なヒル スロープの場合、信頼区間はまったく正確ではありません。シミュレーションの 83.1% でのみ、"95%" 信頼区間に真の値 (4.0) が含まれています。濃度の数値を 2 倍にすることにより [Simulate XY data] ダイアログの 「X値」[X values] タブで X 値の増分を 0.5 から 0.25 に下げる)、この問題を解決します。データ ポイントの数が多いため、シミュレーションの 95.3% で、95% 信頼区間に真の値が含まれています。
シミュレーション ダイアログでさまざまなオプションを選択し、Monte Carlo シミュレーションで効果を確認することで、より良い実験を設計できます。
もう一つの例
ここにt検定の検出力を調べるために、シミュレーションを用いるもう一つの詳細な例があります。
参考文献
1. Arthur Christopoulos, Assessing the distribution of parameters in models of ligand-receptor interaction: to log or not to log, Trends in Pharmacological Sciences, Volume 19, Issue 9, 1 September 1998, 351-357 ページ